사자자리
[암호학] Diffie-Hellman 키 교환 알고리즘 본문
공개키 교환 알고리즘
- 네트워크 같은 공개된 채널에서 키를 교환해도 외부인은 키를 알 수 없게 하는 알고리즘
- 대칭키 암호를 사용하려면, 사전에 수신자와 송신자의 키 교환(Key Exchange)이 이루어져야 한다.
- 대칭키 암호의 안전성은 키에서 비롯되고, 키를 안전하게 공유할 수 없는 환경에서 대칭키 암호는 무용지물이다.
Diffie-Hellman 키 교환의 수학적 원리
1. 모듈로 연산에서의 거듭제곱
2. 페르마의 소정리
3. 이산 로그 문제
1. 모듈로 연산(Modulo Operation)에서의 거듭제곱
https://coding-leo.tistory.com/77
[암호학] 배타적 논리합과 합동식
배타적 논리합(XOR; exclusive or) - 입력으로 들어온 두 인자가 서로 다를 때 참을 반환하는 연산 - 일반적으로 비트 단위로 이뤄진다. 입력 출력 0 0 0 0 1 1 1 0 1 1 1 0 - 임의의 정수를 자기 자신과..
coding-leo.tistory.com
- a, b가 mod m에 대해 합동일 경우, a, b 각각에 정수 x를 더하거나 빼거나 곱해도 여전히 합동이다.

Square and Multiply
- 큰 지수에 대한 합동식을 빠르게 연산하는 알고리즘

2. 페르마의 소정리(Fermat's Little Theorem)

예를 들어, 소수 37과 2, 3, 17은 페르마의 소정리에 따라

을 만족한다.
3. 이산 로그 문제(Discrete Logarithm Problem)

- 5x ≡ 52 (mod 61)를 만족하는 x를 구한다고 생각해보자. 쉽게 떠올릴 수 있는 방법 중 하나는 5를 여러 번 곱해가며 5x (mod 61)을 계산하고, 이 값을 52와 비교하는 것이다. 프로그램으로 구현해서 실행하면 이를 만족하는 x가 21임을 빠르게 알 수 있다.
- 이번에는 m = 2127 - 1, a = 2에 대해 ax ≡ 274877906944 (mod m)을 만족하는 x를 구한다고 생각해보자. 앞에서와 달리 m이 매우 크므로, 식이 성립하는 x를 무차별 대입으로 찾기가 매우 어렵다. 이산 로그 문제를 푸는 방법이 여럿 연구되었지만, 현재까지 알려진 최선의 방법으로도 이 문제를 풀려면 루트 m번 정도의 연산을 해야 한다.
- Diffie-Hellman 알고리즘의 안전성은 이산 로그 문제의 어려움에 바탕을 두고 있다. Diffie-Hellman 키 교환 알고리즘에서 키를 모르는 공격자가 키를 구하려면, m이 22048정도 되는 이산 로그 문제를 풀어야 한다. 이는 현재의 연산능력으로 불가능하다고 알려져 있다.
Diffie-Hellman 키 교환 절차
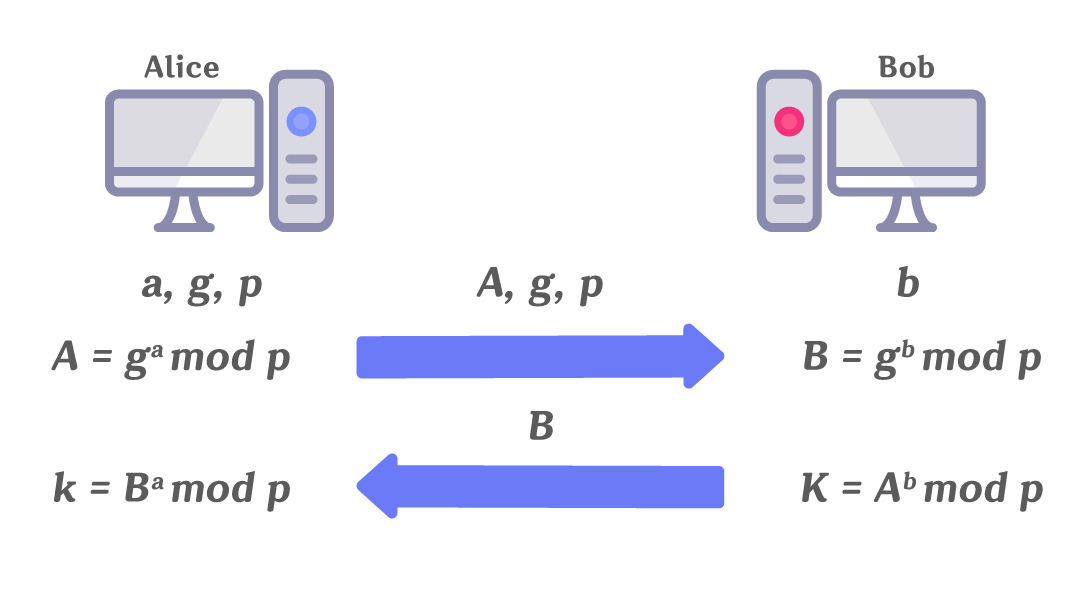
1. Alice는 소수 p와 1 ≤ g ≤ p − 1을 만족하는 적당한 수 g를 정해 Bob에게 전송한다. p는 보통 21024 이상의 큰 소수로 설정한다.
2. Alice는 1 ≤ a ≤ p−1을 만족하는 적당한 수 a를 정하여 A = ga mod p를 Bob에게 전송한다.
3. Alice로 부터 g와 p를 받은 Bob은 1 ≤ b ≤ p−1을 만족하는 적당한 수 b를 정해 B = gb mod p를 Alice에게 전송한다.
4. Alice는 Bob이 보낸 B를 a제곱하여 K ≡ Ba ≡ (gb)a ≡ gba mod p를 계산한다. a와 b의 값이 매우 크지만, 앞에서 소개한 Square and Multipy를 이용하면 쉽게 K의 값을 구할 수 있다.
5. Alice와 Bob은 계산한 K를 통신의 키로 사용한다.
공격자는 둘 사이의 통신을 도청하여 p, g, ga mod p, gb mod p를 알아낼 수 있다.
그러나 이산 로그 문제의 어려움으로 인해, ga mod p로부터 a를 알아내거나, gb mod p로부터 b를 알아내는 것은 불가능하다. 결과적으로 K = gab mod p를 구할 수 없다.
Diffie-Hellman에 대한 중간자 공격
중간자 공격(Man In The Middle attack, MITM)
- 네트워크로 통신하는 두 주체는 서로의 신원을 확인하기 어렵다는 특성을 이용한 능동적 공격
| 수동적 공격 | 공격자가 통신에 개입하지 않는다. | ex) 통신 도청하기 |
| 능동적 공격 | 공격자가 통신에 직접 개입한다. | ex) 통신을 도청하면서 중간에 데이터를 위변조하기 |
Diffie-Hellman에서의 예시

1. Alice와 Bob이 통신을 한다. 공격자는 Alice에게 자신이 Bob이라고 속이고, Bob에게는 자신이 Alice라고 속인다. Alice와 Bob은 통신 대상이 상대방인지, 공격자인지 알 수 없다.
2. Alice가 Bob에게 키 교환을 시도한다. 공격자는 이를 가로채어 둘 모두와 키 교환을 진행한다.
3. 그 결과, Alice와는 K1 키를, Bob과는 K2 키를 공유한다. 공격자에게 속은 Alice와 Bob은 이 사실을 모른다.
4. Alice가 Bob에게 K1 키로 암호화된 데이터를 보내면, 공격자는 이를 복호화할 수 있다. 그리고 복호화된 데이터를 K2 키로 암호화해서 Bob에게 보낼 수 있다. Bob이 Alice에게 데이터를 보낼 때도 이와 같은 방법을 사용한다.
5. 따라서 공격자는 Alice와 Bob 사이에 오가는 정보를 모두 알 수 있고, 이를 변조할 수도 있다.
- 이런 취약점으로 인해, Diffie-Hellman 키 교환은 서로의 신원을 확인할 수 있는 추가적인 매커니즘이 동반되어야 안전하게 이루어질 수 있다.
마치며
타원 곡선 Diffie-Hellman(Elliptic-Curve Diffie-Hellman, ECDH)
- Diffie-Hellman 알고리즘에서 발전한, 더욱 뛰어난 성능을 가진 알고리즘
- 현대 암호의 중요한 주제
- 많은 수학적 지식이 필요하다.
'Dreamhack > 암호학 Cryptography' 카테고리의 다른 글
| [암호학] 블록 암호: 운영 모드 (0) | 2022.08.07 |
|---|---|
| [암호학] 블록 암호: AES (0) | 2022.08.06 |
| [암호학] 블록 암호: DES (0) | 2022.08.06 |
| [암호학] 현대 암호 (0) | 2022.07.31 |
| [암호학] 고전 암호 (0) | 2022.07.31 |




